Пример решения задачи по определению в заданный момент времени t скорости и ускорения точки K – при повороте стрелки механизма стрелочного индикатора с заданными радиусами его шестерён.
Задача
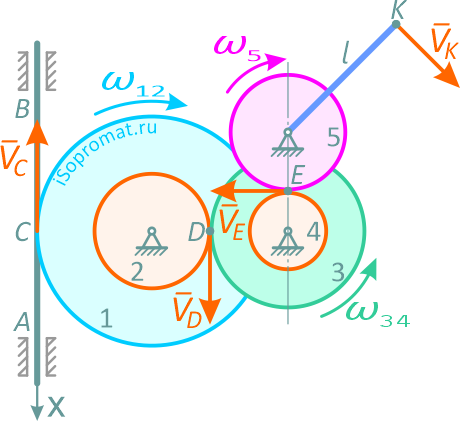
В механизме стрелочного индикатора движение от рейки AB, движущейся в вертикальных направляющих по закону: x=2sinπt см, передается через шестерни 1, 2, 3, 4, 5 стрелке, скреплённой с шестернёй 5; шестерни 2 и 1, 3 и 4 скреплены между собой.
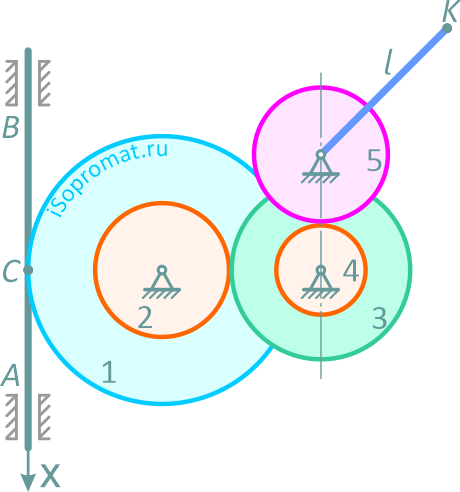
Считая известными радиусы шестерён и длину стрелки l, определить в момент времени t=2/3 с скорость и ускорение точки K – конца стрелки (r1=3 см, r2=1,5 см, r3=2 см, r4=1 см, r5=1,5 см, l=4 см).
Другие примеры решений >
Помощь с решением задач >
Решение
В задаче движение от рейки AB передается через систему шестерен стрелке.
При поступательном движении рейки скорости и ускорения всех ее точек равны и одинаково направлены. Поэтому скорость точки C (точки касания рейки и шестерни 1) может быть определена как производная от закона движения рейки:
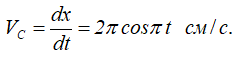
Угловая скорость скрепленных друг с другом шестерен 1 и 2 определится из формулы
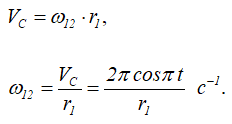
Шестерня 2 находится в зацеплении в точке D с шестерней 3, скрепленной с шестерней 4, поэтому их угловая скорость определяется из соотношения:
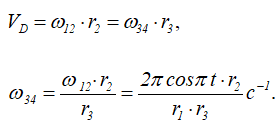
Угловая скорость стрелки и скрепленной с ней шестерни 5 определится из формулы для скорости точки E – точки зацепления шестерен 4 и 5
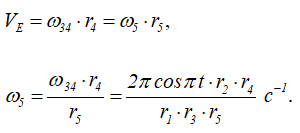
Положительное смещение по оси x стержня определяет и положительное направление вращений всех шестерен.
В нашей задаче в момент времени t=2/3 с скорость точки C равна
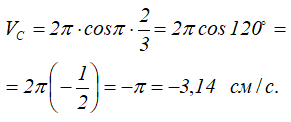
Соответственно с направлением скорости VC, противоположной положительному направлению оси, определяются направления вращения всех шестерен (рисунок 2.9). Для угловой скорости шестерни 5 получим
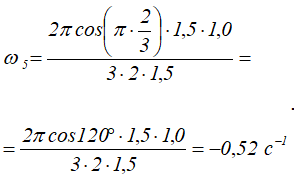
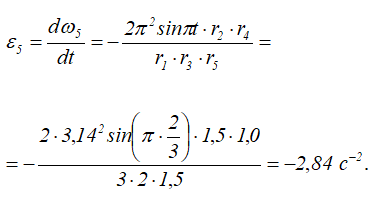
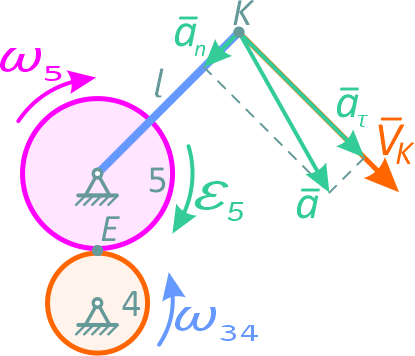
То есть вращение шестерни 5 и стрелки ускоренное (направления ω5 и ε5 совпадают).
Величина скорости точки K (конца стрелки)
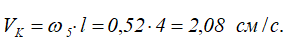
Ускорение точки определяется по формулам (3.11):
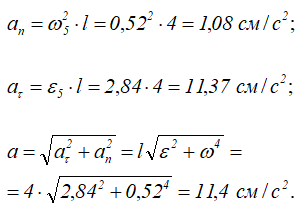
Направление векторов скорости, касательного, нормального и полного ускорения точки K стрелки показано на рисунке 2.10.