Произвольной плоской системой сил называется совокупность сил, линии действия которых находятся в одной плоскости.

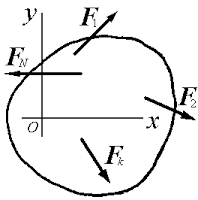
Если все силы, действующие на твердое тело, лежат на одной плоскости, выберем систему координат xOy в плоскости действия сил (рисунок 2.1). В этом случае обнаружим, что

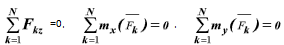
Далее, вспомнив определение момента силы относительно оси, замечаем, что сумма моментов всех сил относительно оси z равна алгебраической сумме моментов этих сил относительно начала координат, т.е. точки О.

В результате останутся следующие три аналитические условия равновесия:

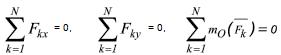
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей x и y и сумма моментов всех сил относительно любой точки, лежащих в плоскости действия сил, были равны нулю.

Главным вектором системы сил называется вектор, равный векторной сумме этих сил:

Главным моментом системы сил относительно точки O тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки:

Примеры решения задач >
Первая форма условий равновесия произвольной плоской системы сил >