Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия систем параллельных и сходящихся сил.
Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.
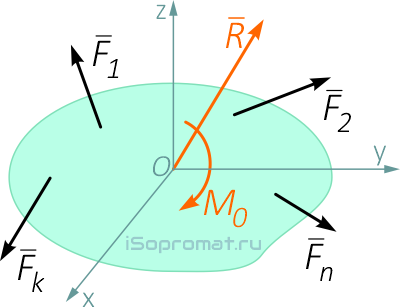
Если система уравновешена, то получаем условия равновесия: R=0, MO=0.
Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:
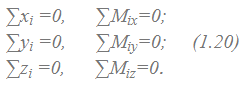
Т.е. суммы проекций всех сил на оси системы координат и суммы моментов относительно этих осей должны быть равны нулю.
Три формы условий равновесия произвольных систем сил
Первая форма равновесия
Для плоской системы сил (например, в плоскости xOy)
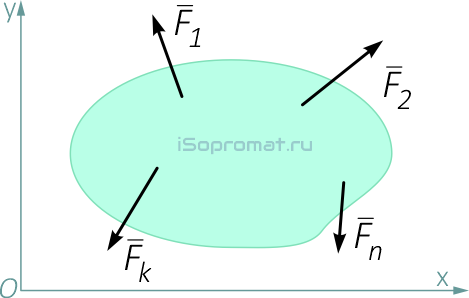
из шести уравнений получаются только три:
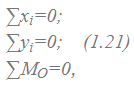
причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно.
Это первая форма уравнений равновесия.
Вторая форма равновесия
Уравнения равновесия могут быть записаны иначе:
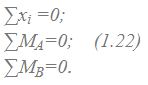
Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.
Третья форма равновесия
Уравнения равновесия произвольной плоской системы сил по третьей форме:
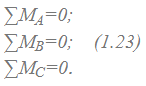
Здесь точки A, B и C не должны лежать на одной прямой.
Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.
Условия равновесия частных случаев
При действии на тело плоской системы параллельных сил
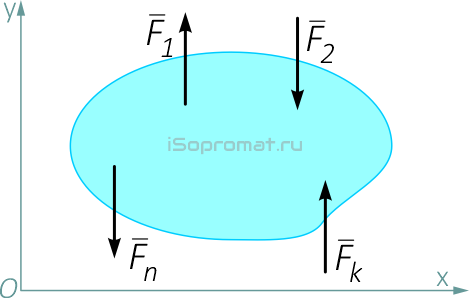
одно из уравнений исчезает и остаются два уравнения:
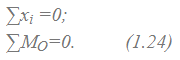
Для пространственной системы параллельных сил
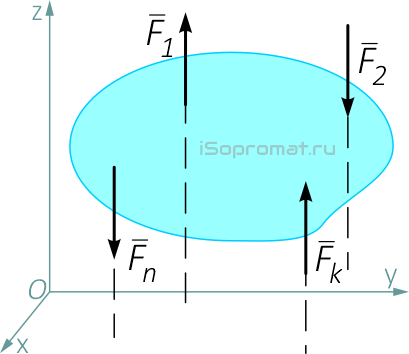
могут быть записаны три уравнения равновесия:
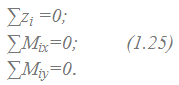
Для системы сходящихся сил (линии действия которых пересекаются в одной точке)
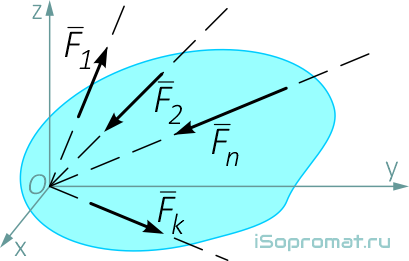
можно написать три уравнения для пространственной системы:
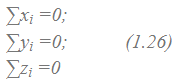
и два уравнения для плоской системы:
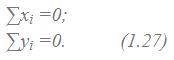
В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.
Далее: