Определять уравновешивающую силу или момент методом Н.Е. Жуковского можно в случаях, когда требуется найти только неизвестную внешнюю силу без определения реакций в кинематических парах, не прибегая к последовательному силовому расчету всего механизма.
Метод основан на принципе возможных перемещений – если система находится в равновесии, то сумма работ внешних сил и моментов на малых возможных перемещениях равна нулю (∑Ai = 0). Так как с помощью сил инерции (по принципу Даламбера) механизм приведен в состояние равновесия, то в данном случае принцип возможных перемещений применим.
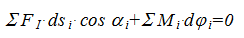
Перейдем к конкретному мгновенному положению механизма, разделив все члены на бесконечно малый промежуток времени (dt), за который происходят указанные малые перемещения:
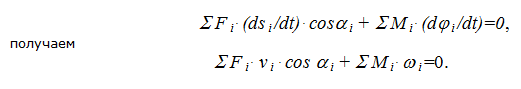
Таким образом, уравнение работ трансформируется в уравнение мгновенных мощностей и принцип возможных перемещений в применении к механизму можно сформулировать следующим образом – если механизм находится в равновесии, то сумма мгновенных мощностей всех внешних сил и моментов, приложенных к звеньям механизма, равна нулю.
Жуковским Н.Е. был предложен метод составления этого уравнения с использованием плана скоростей (рисунок 19).
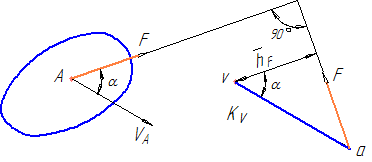
На рисунке 19 изображено некоторое звено, в точке А которого приложена сила F. Скорость VA этой точки изображается на плане скоростей вектором va в масштабе KV.
Перенесем силу F в точку «а» плана скоростей, повернув на 90° (в любую сторону). Возьмем формально момент этой повернутой силы относительно полюса плана скоростей:
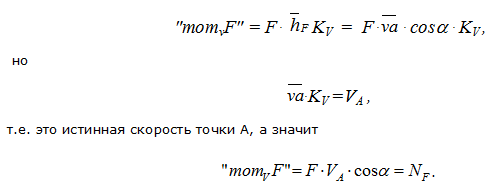
В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.
Таким образом для составления уравнения Жуковского прикладывают все силы, действующие на звенья механизма (включая силы инерции), в соответствующие точки плана скоростей, предварительно повернув их на 90°. Взяв формально сумму моментов этих повернутых сил относительно полюса плана скоростей, фактически получают уравнение развиваемых ими мощностей.
К полученному уравнению добавляют мощности, развиваемые моментами (включая моменты сил инерции).
В уравнение Жуковского мощности должны входить с соответствующими знаками (см. рисунок 16 ). В результате таким приемом фактически получаем мгновенную мощность, развиваемую силой F.
Примечание: для составления уравнения Жуковского можно на повернутый (на 90°) план скоростей прикладывать силы в своем истинном направлении.
Далее: