Рассмотрим порядок построения планов скоростей и ускорений точек звеньев на примере кинематического исследования плоского рычажного механизма (рисунок 1).
Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.
Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное – движение данной точки относительно той, движение которой принято за переносное:
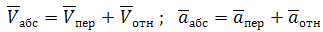
На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана.
На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек.
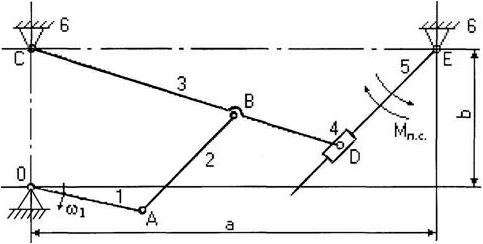
Рисунок 1 – Кинематическая схема плоского рычажного механизма
Рассмотрим построение планов для механизма, представленного на рисунке 1. Вначале рассматривается начальный механизм, а далее решение ведется по группам Ассура в порядке их присоединения.
Начальный механизм:
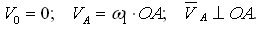
Здесь
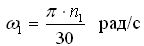
По вычисленному значению VA выбираем масштаб плана скоростей KV и из произвольного полюса откладываем отрезок va изображающий эту скорость:
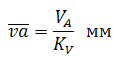
Можно также назначать отрезок va а масштаб KV вычислять:
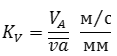
Группа Ассура второго класса 1-го вида (звенья 2, 3):
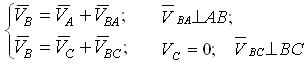
Истинные значения (в м/с) относительных скоростей VBA и VBC определяются после построения плана умножением соответствующих отрезков (в мм) на масштаб плана:
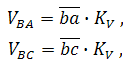
а зная их, можно определить и угловые скорости звеньев 2 и 3:
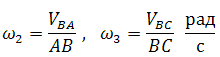
Скорость точки D на плане скоростей можно определить по подобию. (Если известны скорости двух точек одного и того же звена, то скорость любой третьей точки этого же звена можно определить, построив на плане скоростей фигуру, подобную фигуре, образованной этими же буквами на звене механизма). Точки С, В , D на звене 3 лежат на одной прямой. На плане строим отрезок сd, соблюдая условие подобия:
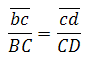
Группа Ассура второго класса 3-го вида (звенья 4,5) :
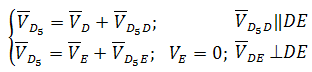
где D5 — точка, находящаяся на звене 5 под точкой D. После определения скорости движения точки D5 относительно точки E можно вычислить угловую скорость звеньев 4 и 5 (ω4=ω5, т. к. эти звенья соединяются поступательной парой):
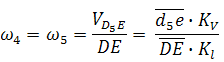
Примечание: в данном случае размер DE является величиной переменной (т.е. в задании он отсутствует), поэтому в каждом положении механизма он определяется через отрезок на чертеже и масштаб длин.
План ускорений строится в таком же порядке.
Начальный механизм
Ускорение точки A состоит только из нормальной составляющей, т.к. задана постоянная угловая скорость первого звена (ω1=соnst):
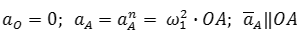
По вычисленному значению ускорения точки A выбирается масштаб плана ускорений и определяется отрезок на плане, соответствующий этому ускорению (или вычисляется масштаб плана ускорений по выбранному отрезку, изображающему ускорение точки A):
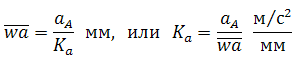
Здесь точка w – полюс плана ускорений.
Группа Ассура (звенья 2,3) второго класса 1-го вида:
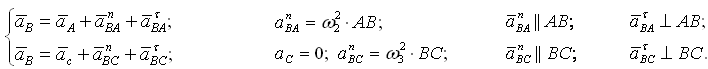
После построения определяются aτBA и aτBC, по которым можно вычислить угловые ускорения звеньев 2 и 3:
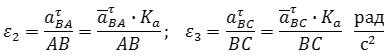
Ускорение точки D определяем по подобию так же, как определяли скорость этой точки:
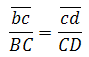
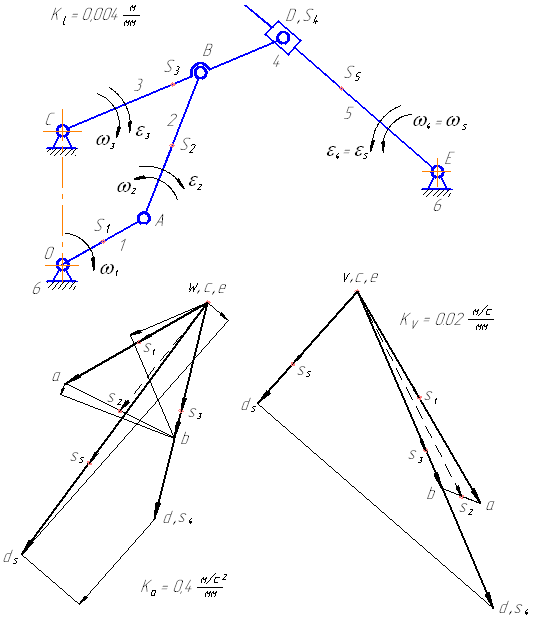
Рисунок 5 – Планы скоростей и ускорений для заданного положения механизма
Группа Ассура (звенья 4,5) второго класса 3-го вида:
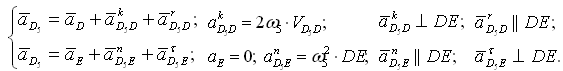
Для определения направления akD5D надо вектор VD5D повернуть на 90° в направлении ω5. Угловые ускорения:
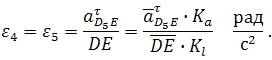
При силовом расчете необходимо иметь ускорения центров масс (asi), которые на плане ускорений определяются методом подобия.
Планы скоростей и ускорений для первого положения заданного механизма приведены на рисунке 5.
Уравнение планов скоростей и ускорений для каждой группы Ассура приведены в таблице 1.
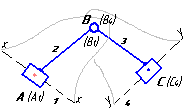
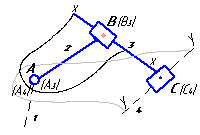
Таблица 1 – Кинематический анализ групп Ассура II класса методом планов
| Вид группы |
Конфигурация
группы |
Уравнения для построения планов скоростей и для определения угловых скоростей | Уравнения для построения планов ускорений и для определения угловых ускорений |
|
1
|
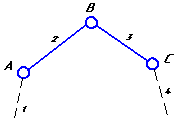 |
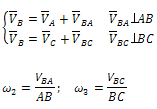 |
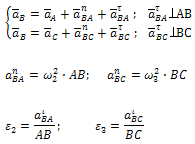 |
| 2 |
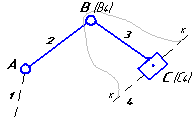 |
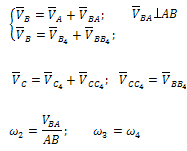 |
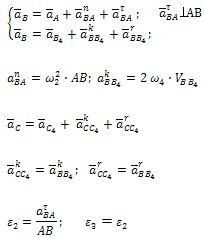 |
| 3 |
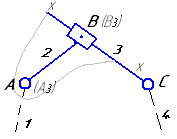 |
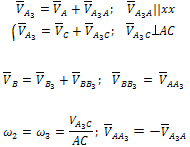 |
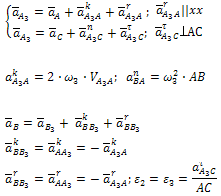 |
| 4 |
 |
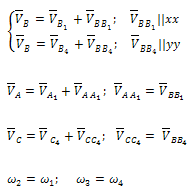 |
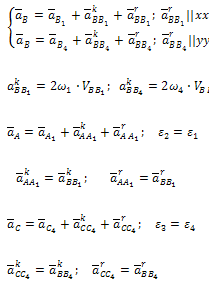 |
| 5 |
 |
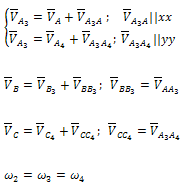 |
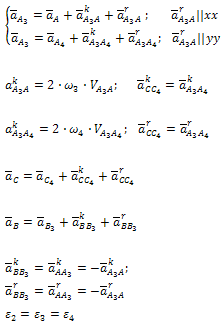 |
Далее: