Ускорение Кориолиса — векторная величина, характеризующая изменение относительной скорости по направлению за счет переносного вращения и изменение величины переносной скорости за счет относительного движения.

Обозначается — a_C

Согласно теореме Кориолиса, абсолютное ускорение точки в сложном движении определяется как геометрическая сумма относительного, переносного и кориолисова ускорений (рис. 3)

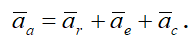
Поскольку, в данном случае, относительное движение происходит по прямой линии, относительное ускорение a_r направлено вдоль этой прямой и определяется выражением

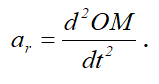
Переносным ускорением точки M является ускорение точки M диска. Диск совершает вращательное движение, следовательно, переносное ускорение определяется выражением

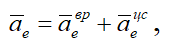
где a_e^вр = ε × OM — вращательное ускорение точки M, направленное перпендикулярно отрезку OM;
a_e^цс = ω² × OM — центростремительное ускорение точки M, направленное к центру диска.

Ускорение Кориолиса или поворотное ускорение определяется по формуле

где ω_e — переносная угловая скорость,
ν_r — относительная скорость точки.

Направление Кориолисова ускорения определяется по правилу векторного произведения или по правилу Жуковского.

Величина ускорения Кориолиса определяется выражением

где α – угол между векторами ω_e и ν_r.

Рассмотрим, какой физический смысл заложен в ускорение Кориолиса. Для простоты будем считать, что диск вращается с постоянной угловой скоростью, а точка M движется относительно диска с постоянной относительной скоростью (рис.4).

Пусть в момент времени t₁ точка M занимала положение M₁ и имела относительную скорость ν_r1. За промежуток времени Δt точка M переместится в положение M₂, при этом направление скорости ν_r изменится вследствие вращения диска. Вектор ν_r получит приращение Δν_r.

Отношение

определяет среднее ускорение точки за промежуток времени Δt.

Предел этого отношения при Δt→0 есть производная

как производная от вектора постоянного по величине.

Рассмотрим, как изменяется переносная скорость в зависимости от относительного движения. В моменты времени t₁ и t₂ переносная скорость определяется выражениями

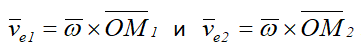
Тогда приращение вектора ν_e за счет относительного движения будет равно

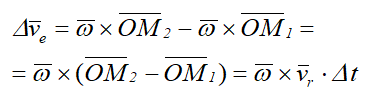
Отношение

в пределе при Δt→0 дает производную

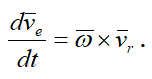
Таким образом, ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.

Абсолютное ускорение точки в сложном движении в общем случае определяется геометрической суммой пяти слагаемых ускорений

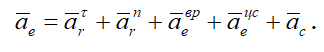
Для определения величины абсолютного ускорения удобнее пользоваться аналитическим методом сложения векторов:

---

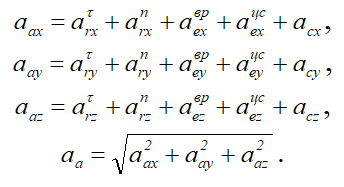
Далее: