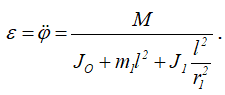Пример решения задачи по определению углового ускорения кривошипа, вращающегося под действием момента M, в эпициклическом механизме, без учета сил трения.
Задача
В эпициклическом механизме (рисунок 4.1) кривошип с противовесом вращается под действием приложенного к нему момента M. Момент инерции кривошипа с противовесом относительно оси его вращения равен J0.
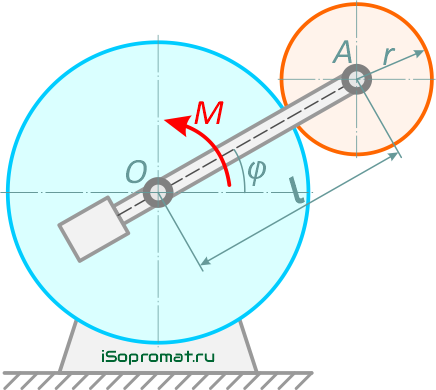
Центр тяжести бегущей шестерни и кривошипа с противовесом находится на оси вращения кривошипа. Расстояние между осями шестерен равно l. Бегающая шестерня имеет радиус r1, массу m1 и момент инерции относительно ее оси J1. Определить, пренебрегая трением, угловое ускорение кривошипа.
Другие примеры решений >
Помощь с решением задач >
Решение
Рассматриваемая система имеет одну степень свободы. За обобщенную координату системы примем угол поворота кривошипа φ, отсчитанный от горизонтали.
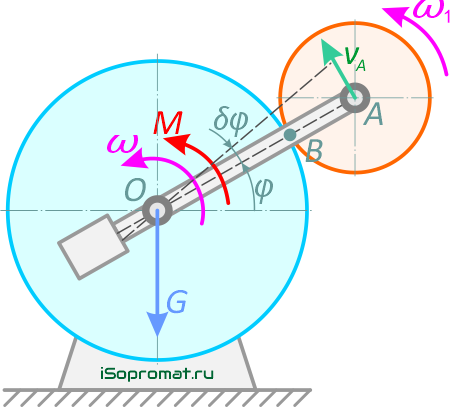
Чтобы воспользоваться уравнением Лагранжа второго рода, определим кинетическую энергию системы как функцию обобщенной координаты φ и обобщенной скорости φ’, равной угловой скорости кривошипа ω.
Кинетическая энергия системы равна сумме кинетической энергии T1 кривошипа с противовесом, вращающегося вокруг неподвижной оси, и кинетической энергии T2 бегающей шестерни, совершающей плоское движение.
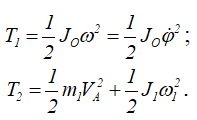
Скорость центра масс шестерни
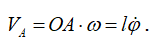
Угловую скорость бегающей шестерни ω1 определим при помощи мгновенного центра скоростей, находящегося в точке B соприкасания шестерен:
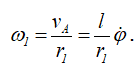
Тогда для T2 получаем
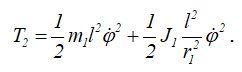
Кинетическая энергия системы
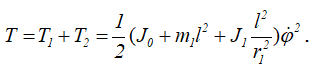
Найдем производные
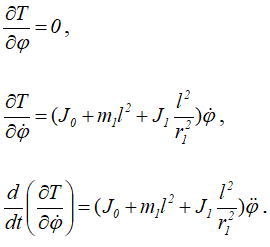
Чтобы найти обобщенную силу Qφ, соответствующую обобщенной координате φ, дадим системе возможное перемещение, сообщив углу φ приращение δφ. Составим сумму элементарных работ задаваемых сил на этом возможном перемещении. В эту сумму войдет только работа вращающего момента, определяемая по формуле
![]()
Обобщенную силу получим по формуле
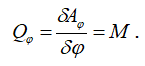
Подставим найденные выражения в уравнение Лагранжа второго рода
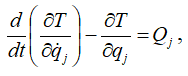
получим
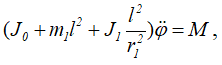
откуда находим угловое ускорение кривошипа